Hilbert zien hotel

Hilbert zien hotel is een gedachte-experiment daor aj een paradoxale, contra-intuïtieve eigenschop van oneindige verzamelings mit kunt deurkriegen. 't Experiment lat zien det een hotel mit een oneindig antal kamers, die allemaolend bezet bint, nog altied neie gasten kan harbargen - oneindig veule zölfs, en dej dit perses töt in de oneindigheid aovernei kunt uutvoeren. 't Idee kwaamp de Duutse wiskundige David Hilbert mit an in een praotien uut 1924, "Über das Unendliche". De netuurkundige George Gamow maakte 't experiment brieder bekend deur zien boek One Two Three... Infinity uut 1947.

Hoe of een oneindig antal neie gasten in een oneindig antal volle hotelkamers kan trekken

De schienbere tegenstelling

Ie gaot uut van een hypothetisch hotel mit een oftelber oneindig antal kamers, die allemaolend bezet bint. Dizze vörm van oneindigheid slat op de netuurlijke getallen, die aj kunt oftellen: $\{0,1,2,\ldots \}.$ Ie zolden mienen det der gien neie gasten in 't hotel kunt trekken. Det zol 't geval wezen bij een eindig antal kamers; dan zol 't doeventilprincipe opgaon (aj $n$ veurwarpen in $m$ deuzen stopt, en $n>m$, dan muj in teminsen iene deuze meer as ien veurwarp doen).

Een eindig antal neie gasten

Prakkezeert det der een neie gast bij 't hotel ankump en een kamer wil. Dan kuw (geliektiedig) de gast die op det moment in kamer iene zit naor kamer tweie verhuzen, de gast in kamer tweie naor kamer dreie, enzowieder. Elke gast giet zo van zien kamer van det moment, n, naor kamer n + 1. Aj det doet, blif kamer iene leug en kan daor de neie gast intrekken. De neie gast zol niet in de leste kamer kunnen trekken: oneindigheid hef ja gien end (gien leste kamer), mar kan wal een begun hebben. Ie kunt dus allennig wat bereiken mit deurschoeven.

Deur dizze warkwieze te herhalen, kuj plekke maken veur elk eindig antal neie gasten. Neemt an det k gasten een kamer wilt. Ie kunt dan alle gasten van kamer n naor kamer n + k verhuzen. Op dezölfde meniere kunt, as k gasten 't hotel wilt verlaoten, alle gasten verhuzen van kamer n naor kamer n − k.

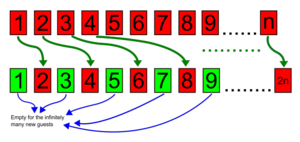
Een oneindig antal neie gasten

Ok een oftelber oneindig antal neie gasten kuj onderbrengen. Ie schoeft de gast in kamer iene naor kamer tweie, de gast in kamer tweie naor kamer viere, en in 't algemien de gast in kamer n naor kamer 2n (tweimaol n). Dan blieft alle oneven kamers (die ok van heurzölf oftelber oneindig bint) leug veur de neie gasten.

't Gedachte-experiment kuj nog wieder ontwikkeln; zo vaalt 't mit verscheiden methodes an te tonen det oftelber oneindige antallen busladings vol oftelber oneindige antallen passagiers allemaolend ondergebracht kunt wörden.

Analyse

Hilbert zien hotel is een waorheidsgetrouwe paradox: ie verkriegt der een contra-intuïtief risseltaot mit det bewiesber waor is. De uutspraoken "der zit iene gast in elke kamer" en "der kunt gien neie gasten bij" bint niet logisch equivalent aj een oneindig antal kamers hebt.

Veureerst kan zo'n toestaand contra-intuïtief lieken. Mar de eigenschoppen van oneindige verzamelings verschilt biester van de eigenschoppen van eindige verzamelings. De paradox van Hilbert zien hotel kuj begriepen mit de theorie van de traansfinitie getallen van de Duutse wiskundige Georg Cantor. In een gewoon (eindig) hotel mit meer as iene kamer, is 't antal kamers mit een oneven nummer vanzölf kleiner as 't totale antal kamers. In Hilbert zien hotel daorentegen is 't antal oneven kamers niet kleiner as 't totale "antal" kamers. Aj 't wiskundig uutdrokt, is de kardinaliteit van de dielverzameling daoras de oneven kamers in zit gelieke an de kardinaliteit van de verzameling van alle kamers. Bij oftelbere verzamelings (verzamelings mit dezölfde kardinaliteit as de netuurlijke getallen) is dizze kardinaliteit $\aleph _{0}$ (alef nul).

Aanders esteld: veur alle oftelber onendige verzamelings is der een bijectieve functie die de oftelber oneindige verzameling an de verzameling netuurlijke getallen koppelt, zölfs as de netuurlijke getallen in de oftelber oneindige verzameling vervat bint. Zo bevat de verzameling rationale getallen - die getallen die aj kunt daleschrieven as een quotiënt van een gehiel getal - de netuurlijke getallen as dielverzameling; toch is dizze verzameling niet groter as de verzameling netuurlijke getallen, umdet de rationale getallen ja oftelber bint: ie hebt een bijectie van de netuurlijke getallen naor de rationale getallen.

Bronnen

• Gamow, George (1947), One Two Three... Infinity: Facts and Speculations of Science, New York: Viking Press
• Hilbert, David (2013), Ewald, William; Sieg, Wilfried (red.), David Hilbert's Lectures on the Foundations of Arithmetics and Logic 1917-1933, Heidelbarg: Springer-Verlag
• Rucker, Rudy (1984) [1982], Infinity and the Mind. The Science and Philosophy of the Infinite, Paladin

Dit artikel is eschreven in 't Zuudwest-Drèents.